Inviten a sus familiares, vecinos y amigos, todos están bienvenidos....Trae tu bicicleta y pasa un día inolvidable, de aprendizaje y diversión,
Los niños deben llegar acompañados de un adulto. Gracias!!
Lugar: Plazoleta central de Bosa (Bosa centro - Alcaldía local- cadel)
Hora de inicio: 9am a 12m
Talleres: 12 a 4 pm
Los esperamos................
Página creada para publicar artículos, experiencias, y trabajos interdisciplinarios, sobre la importancia y el beneficio del uso de la bicicleta como herramienta pedagógica para el desarrollo de aprendizajes ciudadanos significativos.

viernes, 29 de abril de 2011
domingo, 24 de abril de 2011
"LA SOLUCIÓN AL PROBLEMA CLIMÁTICO ES COSA DE NIÑOS"
Son muchas las formas en que podemos contribuir a mitigar los problemas que aquejan a nuestro planeta, si cada uno hace pequeños cambios en sus vidas, empezaríamos a germinar nuevas semillas para mantener los recursos naturales con el equilibrio necesario para seguir existiendo.
domingo, 17 de abril de 2011
ALBERT EINSTEIN EN BICICLETA
www.profisica.com
En una de sus frases más recordadas, Albert Einstein afirmaba con humor y perspicacia que: la vida es como andar en bicicleta, para conservar el equilibrio debes mantenerte en movimiento. La génesis de esta frase no es hecho meramente anecdótico, pues se cuenta que el gran científico era muy aficionado al pedaleo. Incluso se ha dicho que Einstein se encontraba conduciendo una bicicleta cuando descubrió algunas ideas fundamentales que habrían dado forma a su célebre teoría de la relatividad. Sin embargo, más allá de las elucubraciones que le llevaron a revolucionar la física del siglo XX, es evidente que mientras Einstein pedaleaba, su incansable y agudo intelecto debe haber considerado problemas de muy diversa índole. Incluso puedo imaginarlo meditando acerca de alguna curiosa propiedad física de las bicicletas. Una pregunta muy interesante que el ilustre científico podría haberse formulado, y que guarda directa relación con la fotografía que parece abajo, es la siguiente: ¿Por qué se inclina la bicicleta cuando tomamos una curva?

Para intentar responder la interrogante de Einstein con la extensión y el rigor que requiere, antes será necesario introducir un par de nociones de gran importancia en diversos ámbitos de la física: me refiero a los conceptos de torque y centro de gravedad. En relación a este último, cabe señalar que ha sido abordado en otro artículo(1) de modo que solo mencionaré brevemente que, tal como indica su nombre, el centro de gravedad de un objeto es el punto de aquel donde se ejerce la fuerza de gravedad (el peso). En otras palabras, para efectos de determinar el lugar donde actúa la fuerza de gravedad, los cuerpos se comportan como si toda su masa estuviera íntegramente concentrada en un punto al que llamamos centro de gravedad.
Respecto del concepto de torque, también llamado momento de una fuerza o simplemente momento, podemos comenzar definiéndolo como un análogo de las fuerzas para el caso de las rotaciones. En otras palabras, el torque es a las rotaciones como las fuerzas son a las traslaciones. Por ejemplo, si usted desea que un cuerpo en reposo se ponga en movimiento (se traslade), deberá aplicarle una fuerza; lo mismo sucede si desea detener un cuerpo que está en movimiento. En forma equivalente, si usted desea que un objeto experimente una rotación (o que deje de rotar), debe aplicarle un torque.
Regresemos a el profundo interrogante que ocupaba la mente de Einstein mientras pedalea. ¿Por qué se inclina la bicicleta cuando tomamos una curva? De seguro en más de una ocasión se ha encontrado a bordo de un vehículo cuando este toma una cuerva, y en aquel instante habrá experimentado la sensación de que su cuerpo tiende a inclinarse en sentido contrario a la dirección de giro del vehículo. Es decir, mientras el vehículo se mueve en una cierta dirección para tomar la curva, su cuerpo tiende a moverse en la dirección contraria. Para poner un ejemplo menos familiar pero más académico: imaginemos una regla parada sobre uno de sus extremos y haciendo equilibrio en el borde de un disco horizontal. Imagina también que utilizamos una cinta de scoch para sujetar la regla al disco, a modo de bisagra. Si el disco comienza a girar, la regla volteará hacia fuera. La única manera de encontrar un equilibrio y que la regla no voltee ni hacia dentro ni hacia fuera es inclinándola un ángulo preciso en la dirección del eje de rotación. Vale decir, al inclinar hacia dentro la regla, aparece un torque actuando sobre ella en su centro de gravedad, y que es producido por su peso. Con la bicicleta ocurre exactamente lo mismo. Las siguientes figuras muestran la situación real y una representación idealizada. En el lado izquierdo se muestran dos figuras que actúan sobre Einstein y su bicicleta: el peso (fuerza de gravedad), y la fuerza de roce entre el suelo y la rueda delantera(2). Por simplicidad, en el lado derecho se considera que Einstein junto a con la bicicleta forman un solo cuerpo rígido y extenso en forma de óvalo, provisto de una sola rueda, y cuyo punto de contacto con el suelo corresponde al lugar donde se ejerce la fuerza de roce. En ambas ilustraciones se observa que el conjunto bicicleta-Einstein forma un cierto ángulo de inclinación respecto de la vertical.
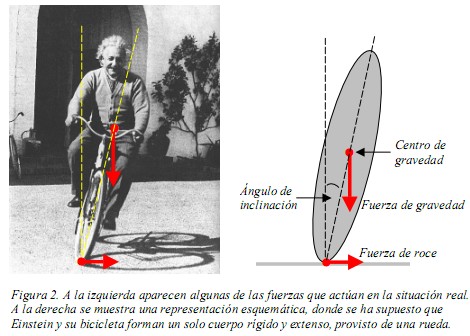
Si las suposiciones anteriores le parecen extrañas o poco realistas, debo decir en mi defensa que es practica habitual es física hacer abstracción de todos los elementos accesorios de un problema, para centrar la atención exclusivamente en lo relevante. Desde luego, no se me ha cruzado por la mente insinuar que el buen Einstein sea un personaje irrelevante, pero como el ilustre científico sabía muy bien, debemos ser sumamente cuidadosos al momento de decidir cuales ingredientes incorporar en un problema. ¿Cómo saber qué ingredientes debemos incluir y cuales descartar? Bueno, por desgracia no existe una receta. Un cocinero y un físico adquieren su buen gusto y su olfato como resultado de un trabajo arduo y prolongado.
Regresando a la figura 2, observamos que el peso se ejerce en el centro de gravedad del conjunto bicicleta-Einstein. Usando una analogía como una bisagra, el centro de gravedad hace las veces de manilla, mientras el peso es el equivalente de nuestra mano, tirando del conjunto hacia el suelo. Con ello se explica claramente la necesidad de la inclinación de la bicicleta, pues el torque debido al peso tiende a girarla hacia el lado derecho de la figura, contrarrestando de este modo su tendencia a rotar en sentido contrario, producto de la curva tomada por Einstein. Sin embargo, esto genera una nueva pregunta: ¿Por qué la bicicleta no cae, dado que se encuentra inclinada? Pues bien, la solución del problema comienza a vislumbrarse al constatar que si la bicicleta no se encontrara en movimiento y tomando una curva, esta caería al suelo. Por otra parte, debemos recordar que para anular un torque se requiere de otro que posea igual magnitud pero sentido contrario al primero. ¿Cuál es el torque que anula el efecto del peso sobre la bicicleta? Si miramos atentamente la figura 2 una vez más, descubriremos que la respuesta nos la entrega la fuerza de roce, la que a su vez es consecuencia de la curva que la bicicleta está tomando, pues de no ser por la maniobra de giro efectuada por Einstein, el roce en dirección al centro de giro no existiría. En efecto, siendo majadero, si usamos una vez más ala analogía con la puerta, es fácil convencerse de que la fuerza de roce ejerce un torque en sentido contrario al que produce la fuerza de gravedad, pues mientras esta última tiende a hacer que la bicicleta caiga al suelo, el roce tiende a girar la bicicleta en sentido contrario, contrarrestando el peso y evitando la caída. Naturalmente, existe un ángulo preciso que permite que los torques se equilibren y que la bicicleta no voltee ni hacia fuera ni hacia dentro (ver el apéndice).
Pero además de oponerse al torque producido por la fuerza de gravedad, el roce cumple otra función de suma importancia en el problema que nos ocupa, pues ella es la que provee la fuerza necesaria para tomar una curva. Para entender este punto de forma intuitiva, imaginemos que la bicicleta se mueve en línea recta y que repentinamente el buen Einstein intenta tomar una curva sobre un tramo del camino que se encuentra aceitado o cubierto de hielo; obviamente, la bicicleta se deslizará y seguirá moviéndose en línea recta, mientras que el destino más probable de nuestro ilustre ciclista será terminar en el suelo después de sufrir una estrepitosa caída. Vemos entonces que el roce aparece como resultado de la curva tomada por la bicicleta, produciendo la fuerza que permite que esta se desvía de su trayectoria rectilínea. Además, cabe mencionar que el roce siempre tiene la dirección y el sentido del centro de giro. En este contexto decimos que el roce ejerce una fuerza centrípeta, porque apunta hacia el centro. Y dado que el viaje de Einstein en bicicleta está llegando a su fin, no está demás señalar que las conclusiones que hemos obtenido son aplicables tanto a una bicicleta como a una moto, o a cualquier otro vehículo de similares características.
Naturalmente, considero poco probable que Einstein hubiese abordado el problema que nos ocupa con la extensión y la minuciosidad que nosotros le hemos dedicado, pues su aguda intuición y su extraordinario dominio de la física seguramente le habrían conducido a la respuesta en fracción de segundo, dejando su mente en libertad para considerar otros problemas, o quizá para concentrarse en el pedaleo, mantenerse en movimiento y no perder el equilibrio.
¿Quieres saber más?
La siguiente figura (Fig. 3) muestra el conjunto bicicleta-Einstein en forma de óvalo analizado antes, pero en este caso se han incorporado todas las fuerzas en juego, además del ángulo de inclinación 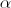 respecto de la vertical. Vemos que el peso
respecto de la vertical. Vemos que el peso 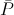 se ejerce en el centro de gravedad del sistema. Se observa también que en el punto de contacto entre la rueda y el suelo actúan la fuerza normal
se ejerce en el centro de gravedad del sistema. Se observa también que en el punto de contacto entre la rueda y el suelo actúan la fuerza normal 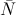 y la fuerza de roce
y la fuerza de roce 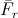 . Como se ha mencionado antes, esta última es la que proporciona la fuerza centrípeta que permite a la bicicleta tomar la curva. La fuerza designada como
. Como se ha mencionado antes, esta última es la que proporciona la fuerza centrípeta que permite a la bicicleta tomar la curva. La fuerza designada como 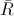 es la reacción del piso y corresponde a la suma vectorial de las fuerzas de roce y normal.
es la reacción del piso y corresponde a la suma vectorial de las fuerzas de roce y normal.
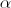 respecto de la vertical. Vemos que el peso
respecto de la vertical. Vemos que el peso 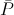 se ejerce en el centro de gravedad del sistema. Se observa también que en el punto de contacto entre la rueda y el suelo actúan la fuerza normal
se ejerce en el centro de gravedad del sistema. Se observa también que en el punto de contacto entre la rueda y el suelo actúan la fuerza normal 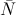 y la fuerza de roce
y la fuerza de roce 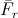 . Como se ha mencionado antes, esta última es la que proporciona la fuerza centrípeta que permite a la bicicleta tomar la curva. La fuerza designada como
. Como se ha mencionado antes, esta última es la que proporciona la fuerza centrípeta que permite a la bicicleta tomar la curva. La fuerza designada como 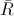 es la reacción del piso y corresponde a la suma vectorial de las fuerzas de roce y normal.
es la reacción del piso y corresponde a la suma vectorial de las fuerzas de roce y normal.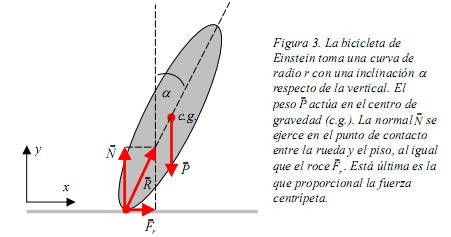
La dirección de 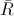 coincide con la inclinación de la bicicleta, de modo que la proyección de este vector pasa por el centro de gravedad del sistema. Esto último puede no resultar evidente para muchos lectores, así que dejaremos la demostración para el final de la discusión. Por de pronto, apelo a la confianza de mis amables lectores. Aclarando este punto, estamos en condiciones de aplicar la segunda ley de Newton al problema que nos ocupa, notando que a partir de la figura 2 podemos escribir las siguientes igualdades:
coincide con la inclinación de la bicicleta, de modo que la proyección de este vector pasa por el centro de gravedad del sistema. Esto último puede no resultar evidente para muchos lectores, así que dejaremos la demostración para el final de la discusión. Por de pronto, apelo a la confianza de mis amables lectores. Aclarando este punto, estamos en condiciones de aplicar la segunda ley de Newton al problema que nos ocupa, notando que a partir de la figura 2 podemos escribir las siguientes igualdades:
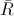 coincide con la inclinación de la bicicleta, de modo que la proyección de este vector pasa por el centro de gravedad del sistema. Esto último puede no resultar evidente para muchos lectores, así que dejaremos la demostración para el final de la discusión. Por de pronto, apelo a la confianza de mis amables lectores. Aclarando este punto, estamos en condiciones de aplicar la segunda ley de Newton al problema que nos ocupa, notando que a partir de la figura 2 podemos escribir las siguientes igualdades:
coincide con la inclinación de la bicicleta, de modo que la proyección de este vector pasa por el centro de gravedad del sistema. Esto último puede no resultar evidente para muchos lectores, así que dejaremos la demostración para el final de la discusión. Por de pronto, apelo a la confianza de mis amables lectores. Aclarando este punto, estamos en condiciones de aplicar la segunda ley de Newton al problema que nos ocupa, notando que a partir de la figura 2 podemos escribir las siguientes igualdades: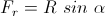 (1)
(1)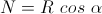 (2)
(2)A partir de (1) y (2), y efectuando sumatoria de fuerzas separadamente sobre los ejes x e y resulta:
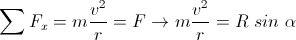 (3)
(3)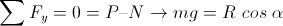 (4)
(4)En estas ecuaciones, v es la velocidad al tomar la curva, m es la masa del conjunto bicicleta-Einstein, y r es el radio de giro. Si ahora dividimos miembro a miembro las ecuaciones (3) y (4) se obtiene:
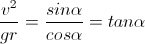
Por lo tanto,
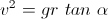
Esta ecuación nos proporciona valiosa información acerca de la bicicleta y su ilustre conductor. Nos dice, por ejemplo, que el ángulo de inclinación 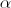 es independiente de la masa, y que a mayor velocidad, más inclinada debe encontrarse la bicicleta. También nos dice que para una rapidez fija, cuanto menor es el radio de giro, mayor deberá ser
es independiente de la masa, y que a mayor velocidad, más inclinada debe encontrarse la bicicleta. También nos dice que para una rapidez fija, cuanto menor es el radio de giro, mayor deberá ser 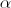 .
.
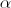 es independiente de la masa, y que a mayor velocidad, más inclinada debe encontrarse la bicicleta. También nos dice que para una rapidez fija, cuanto menor es el radio de giro, mayor deberá ser
es independiente de la masa, y que a mayor velocidad, más inclinada debe encontrarse la bicicleta. También nos dice que para una rapidez fija, cuanto menor es el radio de giro, mayor deberá ser 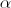 .
.Ahora demostremos que la proyección del vector 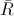 para por el centro de gravedad del conjunto bicicleta-Einstein. Para ello, supondremos que
para por el centro de gravedad del conjunto bicicleta-Einstein. Para ello, supondremos que 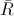 forma un ángulo distinto de
forma un ángulo distinto de 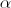 respecto de la vertical, al que designaremos por
respecto de la vertical, al que designaremos por 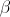 . Además, vamos a efectuar sumatoria de torques respecto del centro de gravedad del sistema. En estas condiciones, el torque ejercido por el peso es nulo. Llamemos d a la distancia desde el centro de gravedad hasta el punto de contacto de
. Además, vamos a efectuar sumatoria de torques respecto del centro de gravedad del sistema. En estas condiciones, el torque ejercido por el peso es nulo. Llamemos d a la distancia desde el centro de gravedad hasta el punto de contacto de 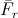 y
y 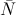 con el suelo. Como los torques efectuados por estas dos fuerzas se anulan, resulta:
con el suelo. Como los torques efectuados por estas dos fuerzas se anulan, resulta:
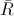 para por el centro de gravedad del conjunto bicicleta-Einstein. Para ello, supondremos que
para por el centro de gravedad del conjunto bicicleta-Einstein. Para ello, supondremos que 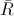 forma un ángulo distinto de
forma un ángulo distinto de 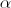 respecto de la vertical, al que designaremos por
respecto de la vertical, al que designaremos por 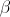 . Además, vamos a efectuar sumatoria de torques respecto del centro de gravedad del sistema. En estas condiciones, el torque ejercido por el peso es nulo. Llamemos d a la distancia desde el centro de gravedad hasta el punto de contacto de
. Además, vamos a efectuar sumatoria de torques respecto del centro de gravedad del sistema. En estas condiciones, el torque ejercido por el peso es nulo. Llamemos d a la distancia desde el centro de gravedad hasta el punto de contacto de 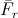 y
y 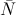 con el suelo. Como los torques efectuados por estas dos fuerzas se anulan, resulta:
con el suelo. Como los torques efectuados por estas dos fuerzas se anulan, resulta: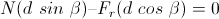
Introduciendo las ecuaciones (1) y (2) se obtiene:
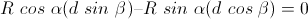
Factorizando y empleando una conocida identidad trigonométrica:
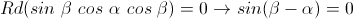
Pero el seno de un ángulo sólo se anula cuando su argumento también se anula, de modo que:
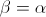
Tal como habíamos anticipado, la proyección del vector 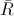 pasa necesariamente por el centro de gravedad del sistema.
pasa necesariamente por el centro de gravedad del sistema.
Jorge Pinochet I.Licenciado en Física, Universidad Católica de Chile. pasa necesariamente por el centro de gravedad del sistema.
pasa necesariamente por el centro de gravedad del sistema.
Suscribirse a:
Comentarios (Atom)
